https://www.acmicpc.net/problem/25210

접근 방식
먼저, 정사각형의 꼭짓점이 될 수 있는 구간을 정한다.
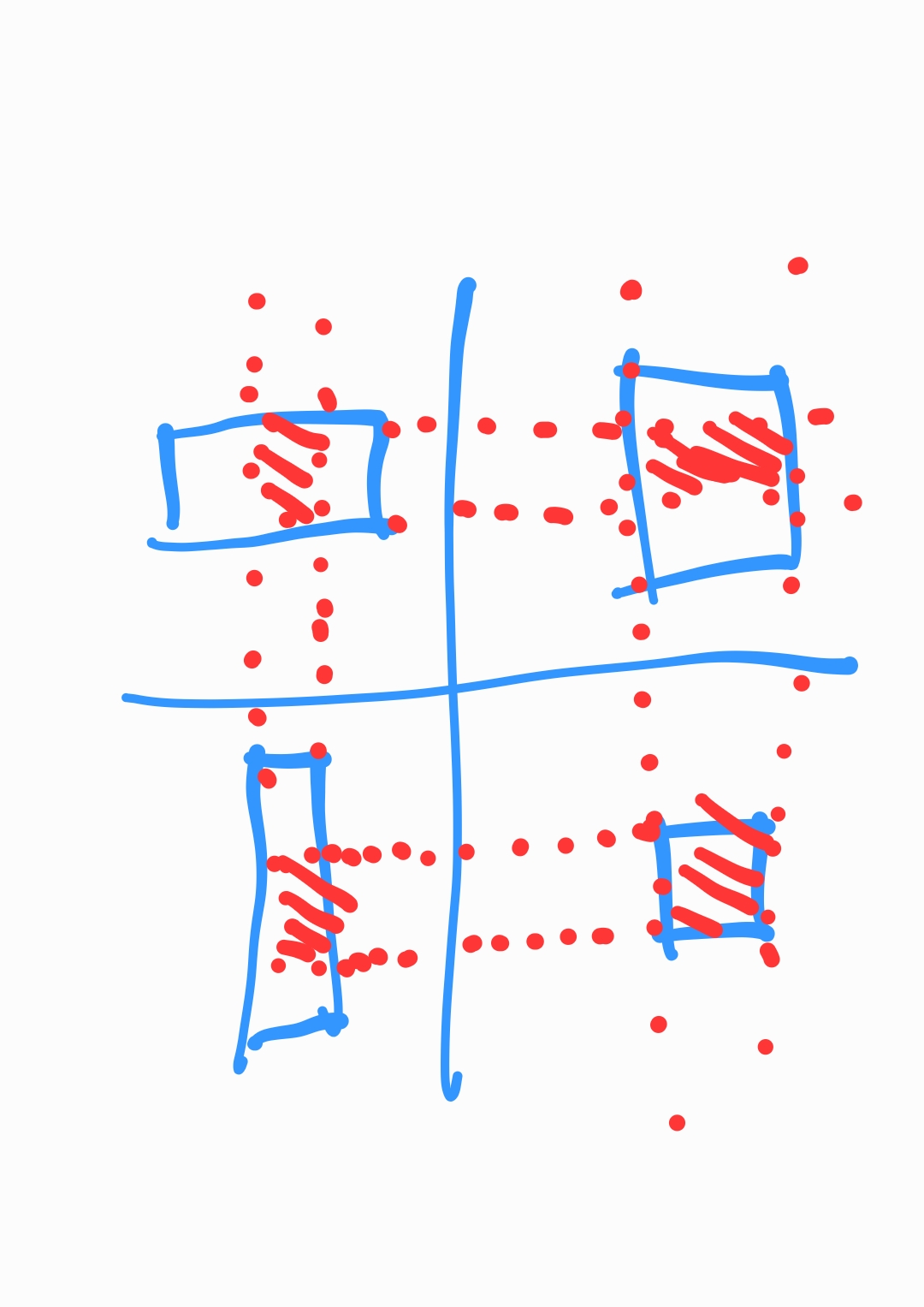
회전하지 않은 정사각형이 되야 하기 때문에, 빨간색 외의 부분은 점으로 선택되지 못한다. 따라서 이러한 부분을 없애준다.
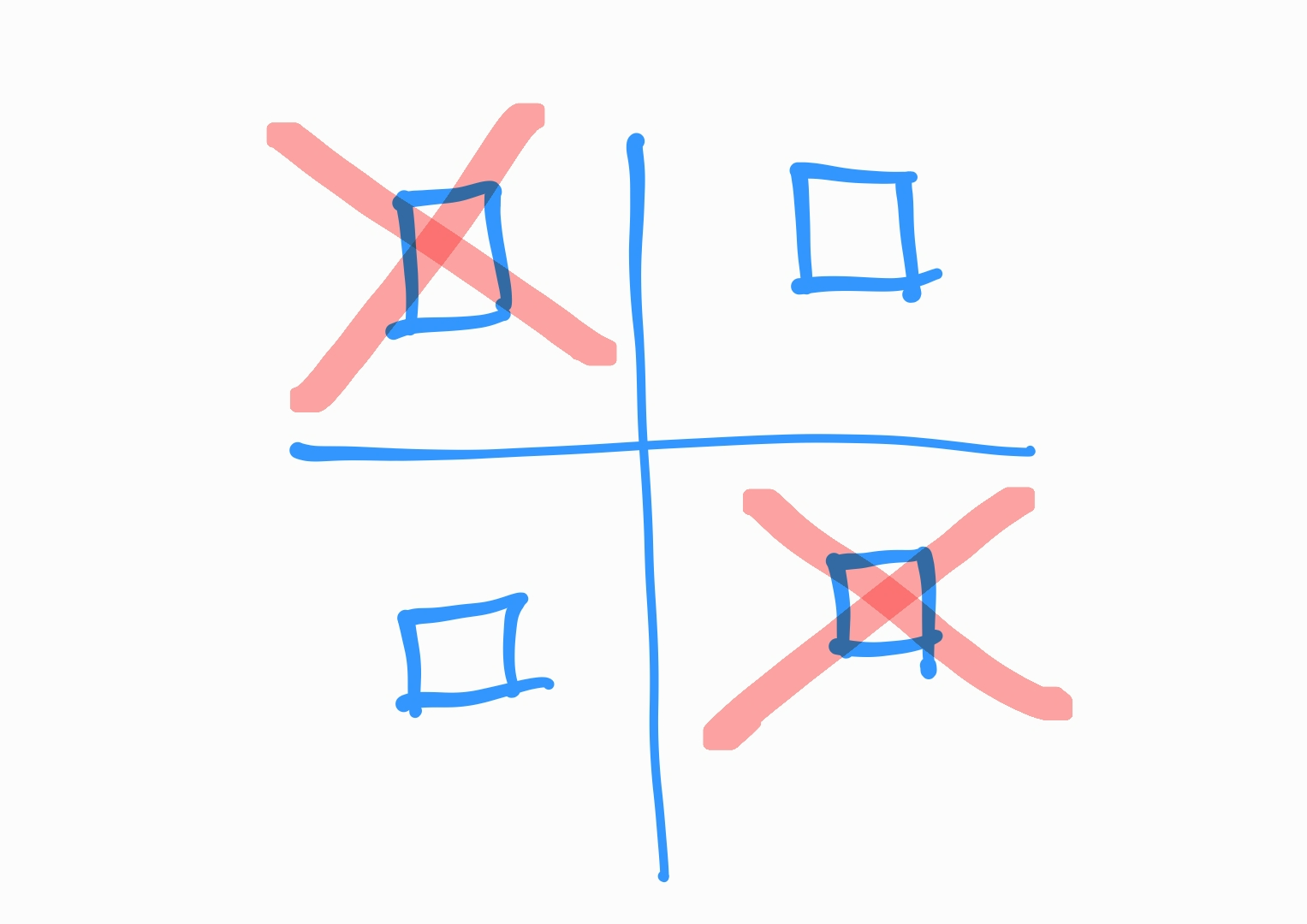
두번째로 남은 부분에서, 좌 우 상 하 범위를 한정시켜 놨기 때문에, 1사분면과 3사분면만 생각해준다.
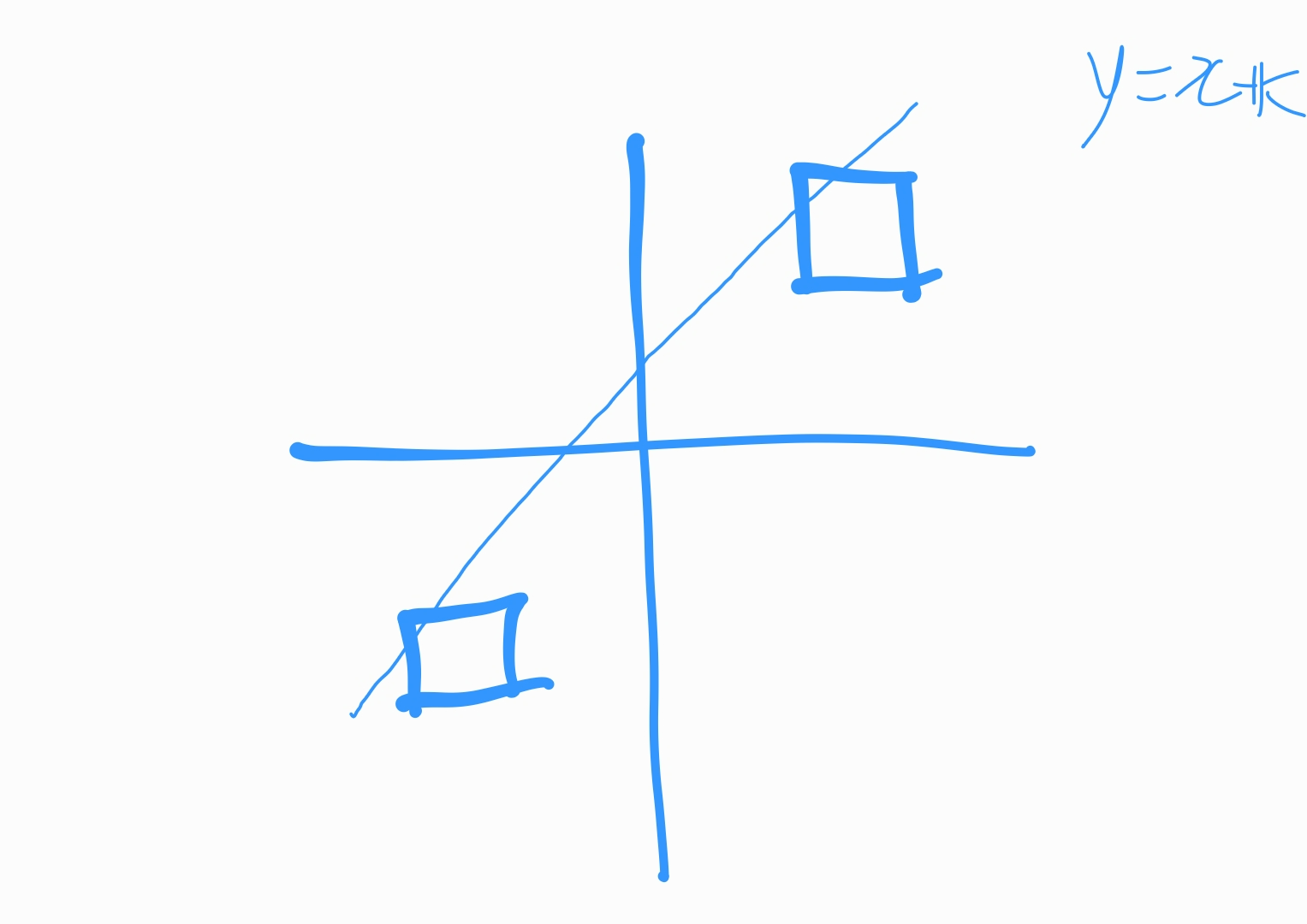
마지막으로 정사각형을 만들기 위해서, y=x+k(k는 문제의 범위인 -100000~100000) 형태의 그래프를 그려준다. 이 그래프가 1사분면의 정사각형에서 만나는 점 N개, 3사분면 정사각형에서 만나는 점 M개가 있다면, 이 때 그릴수 있는 정사각형의 개수는 N*M개 일 것이다.
이러한 과정을 모든 K에 대해서 해준 후 계산을 하면 답을 구할 수 있다.
코드
#include<iostream>
#include<algorithm>
#include<tuple>
using namespace std;
tuple<int, int, int, int> square[5];
int leftx1, leftx2, rightx1, rightx2, topy1, topy2, boty1, boty2;
long long counter;
void check(int k) { //y=x+k 대각선에 겹치는 점의 갯수 세기
//1사분면
long long count1, count2;
int y1 = min(rightx2 + k,topy1);
int y2 = max(rightx1 + k,topy2);
if (y2 > y1)count1 = 0; //이러한 경우는 1사분면에서 그래프와 사각형이 만나지 못 한 경우
else count1 = y1-y2+1;
//3사분면
int y3 = max(leftx1 + k, boty2);
int y4 = min(leftx2 + k, boty1);
if (y3 > y4)count2 = 0; //이러한 경우는 3사분면에서 그래프와 사각형이 만나지 못 한 경우
else count2 = y4-y3+1;
counter += count1 * count2;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
for (int i = 1; i <= 4; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
square[i] = { x1,y1,x2,y2 };
}
rightx1 = max(get<0>(square[1]), get<0>(square[4]));
rightx2 = min(get<2>(square[1]), get<2>(square[4]));
leftx1 = max(get<2>(square[2]), get<2>(square[3]));
leftx2 = min(get<0>(square[2]), get<0>(square[3]));
topy1 = min(get<3>(square[1]), get<3>(square[2]));
topy2 = max(get<1>(square[1]), get<1>(square[2]));
boty1 = min(get<1>(square[3]), get<1>(square[4]));
boty2 = max(get<3>(square[3]), get<3>(square[4]));
for (int i = -100000; i <= 100000; i++)check(i);
cout << counter;
}
생각이 꽤 많이 필요한 문제였다고 생각한다.
도형들을 보고 함수를 이용할 생각을 하기가 어려웠다.
'알고리즘 > IUPC 2022' 카테고리의 다른 글
| [백준] 25216번 파밍루트 [C++] (0) | 2022.05.30 |
|---|---|
| [백준] 25208번 새벽의 탐정 게임 [C++] (0) | 2022.05.24 |
| [백준] 25215번 타이핑 [C++] (0) | 2022.05.24 |
| [백준] 25212번 조각케이크 [C++] (0) | 2022.05.24 |
| [백준] 25214번 크림 파스타 [C++] (0) | 2022.05.24 |



