https://www.acmicpc.net/problem/1005
문제

접근 방법
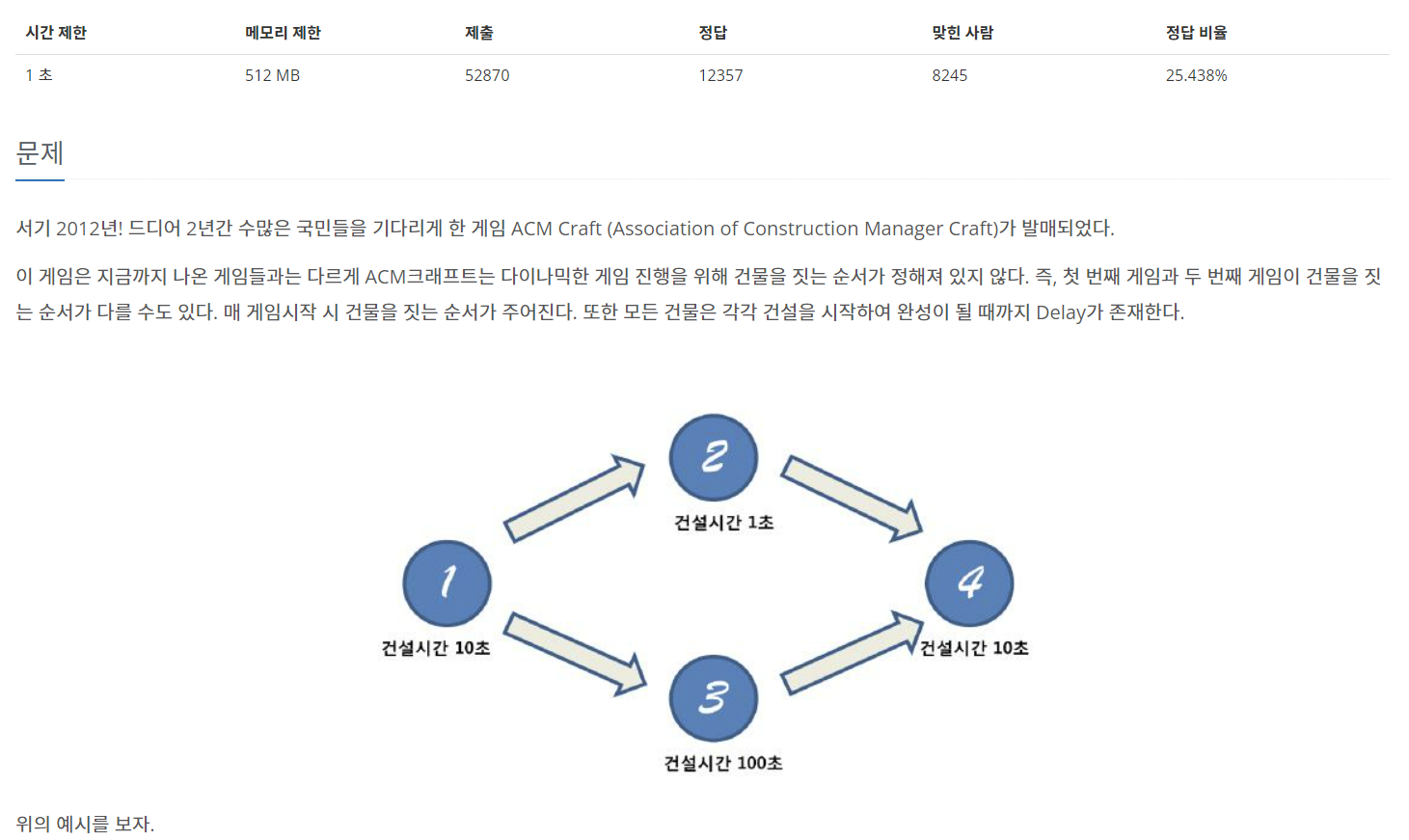
위의 그림을 예시로 들어 설명하자면 , 3번을 짓기 위해서는 1번이 선행적으로 건설이 되어 있어야 한다.
이러 한 경우에 3번까지 짓는데 걸리는 시간은 1번을 짓는데 걸리는 시간+3번을 짓는데 걸리는 시간이 된다.
4번을 짓기 위해서는 2번과 3번이 선행적으로 건설이 되어 있어야 한다.
여기서 2번을 짓는데까지 걸리는 시간과, 3번을 짓는데까지 걸리는 시간이 다를텐데, 두개 다 완성이 되어야 4번 건설 시작이 가능하므로 둘 중 큰 값을 구해야 한다.
따라서 max(2번까지 걸리는 시간,3번까지 걸리는시간)에 4번을 짓는데 걸리는 시간이 4번까지 짓는데 걸리는 시간이다.
이러한 식으로 X번 건물을 지을 때 선행적으로 지어야 하는 건물이 총 N개라면, N개중에서 가장 오래 걸리는 시간과 X번 건물 짓는데 걸리는 시간을 더해 준 값이 X번 까지 짓는데 걸리는 시간이 된다.
이러한 식으로 원하는 답을 구할 수 있다.
코드
#include<iostream>
#include<queue>
#include<cmath>
#include<unordered_set>
#include<string>
#include<stack>
#include<vector>
using namespace std;
int n,m;
int t[1001];//해당 건물을 짓는데 걸리는 시간
int dp[1001];//해당 건물까지 짓는데 걸리는 시간
vector<int> v[1001];//해당 건물의 선행 건물들을 벡터에 넣는다.
int dpf(int d) {
if (dp[d] != -1)return dp[d];
int maxint = 0;
for (int i = 0; i < v[d].size(); i++) {
maxint = max(dpf(v[d][i]), maxint); //선행 건물 중 가장 큰 값을 구함
}
dp[d] = maxint + t[d];
return dp[d];
}
int main() {
ios::sync_with_stdio(false);
int test;
cin >> test;
for (int c = 0; c < test; c++) {
cin >> n >> m;
for (int i = 1; i <= n; i++) { cin >> t[i];
dp[i] = -1;
v[i].clear();
}
for (int i = 0; i < m; i++) {
int x, y;
cin >> x >> y;
v[y].push_back(x);
}
cin >> m;
cout << dpf(m)<<'\n';
}
}
알고리즘의 분류가 DP임을 안 상태에서 문제를 풀어서 간단하게 생각 할 수 있었다.
'알고리즘' 카테고리의 다른 글
| [백준] 1948번 임계경로 [C++] (0) | 2022.05.02 |
|---|---|
| [백준] 1766번 문제집 [C++] (0) | 2022.05.02 |
| [백준] 1167번 트리의 지름 [C++] (0) | 2022.04.30 |
| [백준] 2206번 벽 부수고 이동하기 [C++] (0) | 2022.04.29 |
| [백준] 1937번 욕심쟁이 판다 [C++] (0) | 2022.04.29 |



